

| author | David Leal |
| version | 2.0 |
| date | 2000-02-21 |
| circulation | Ray Goult, Phil Kraushar, Keith Hunten, PDES Inc Modules Development Team, ISO TC184/SC4/WG12 |
| 1 | 2000-01-21 | initial draft for review at the Melbourne meeting of ISO TC184/SC4/WG12 |
| 2 | 2000-02-21 | revised draft following comments in Melbourne, especially from Martin Philipp (editor of ISO 10303-214) and Julian Fowler (editor of ISO 10303-43) |
A large part of the Engineering Analysis Core Model (ISO 10303-107) is concerned with the identification or description of property distributions by mathematical functions. A property distribution can be:
There are many different approaches used in engineering for the description of property distributions. For example, a property distribution can be described using a mesh, as in finite element analysis, or using an n-dimensional b-spline (a generalisation of the mathematical techniques used in CAD systems for geometry). Whatever the approach, the property distribution is described by a mathematical function.
The Mathematical Constructs Schema (ISO 10303-50) has a comprehensive capability for the exchange of information about mathematical functions. However this part does not specify how mathematical functions are used to describe a property distribution. At present, there is no link between ISO 10303-50 and the rest of STEP.
The EACM has defined information requirements for the description of property distributions. The first approach to the interpretation of these requirements proposed:
The review carried out by TC184/SC4/WG12 in Melbourne found that the entity general_property corresponds solely to property_space in the EACM. A new integrated resource entity is required to correspond to property_value in the EACM.
The review carried out by TC184/SC4/WG12 in Melbourne also found that the relationships between property_space and maths_space, and between property_value and maths_value, do not correspond closely to representation as defined in part 43. It was concluded that a new part 5x should be created to provide the link to part 50, and that the entities in this new part should not be subtypes of existing entities in part 43.
This document summarises the proposed extensions to the existing STEP integrated resources, and explains the reason for them. The extensions may be the basis for a new STEP part 5x. The extension will enable future APs, such as the proposed Fluid Dynamics AP, to make use of the Mathematical Constructs Schema in ISO 10303-50.
TERMINOLOGY - In this document, the relationship between a property value and a mathematical value is referred to as 'identification'. Hence the temperature value 20 degrees Celsius is 'identified by' the real value 20.0, with respect to the Celsius scale.
The term 'identification' is also used for the relationship between a point within a product or state within an action and a mathematical value. In this case, the point or state is identified with respect to a particular parameterisation.
Consider the product_definition that is 'widget type XYZ'. A record of the fact that:
each widget of type XYZ has a mass in the range 9.99 to 10.01 Kg
is a property_definition.
Using ISO 10303-41, it is not possible to separate the existence of the abstract concept:
the mass range 9.99 to 10.01 Kg
from the relationship with widget type XYZ.
The introduction of an entity property_value, makes this possible as shown in Figure 1.
Figure 1: Property of a single thing
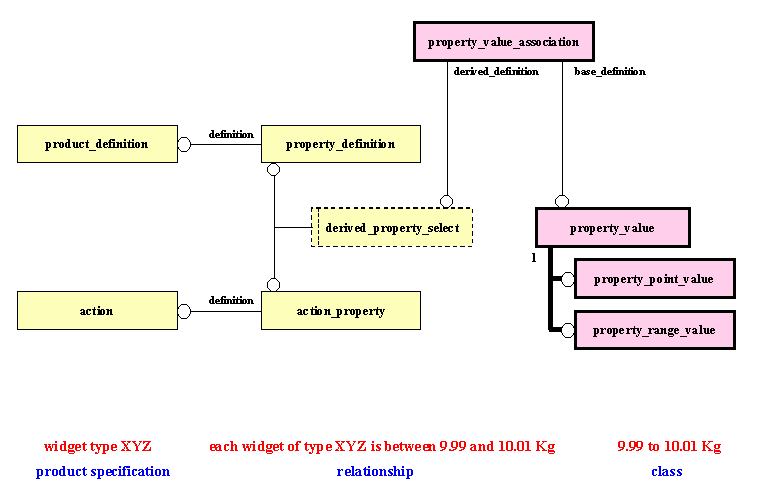
Notes:
This is a trivial example, which can be instantiated perfectly well using part 41 without the entity property_value. The reason for this more elaborate approach will become apparent when a property distribution and its identification is considered.
The entities property_value_association and property_value
are directly analogous to the entities general_property_association and
general_property in ISO 10303-41 edition 2. These extensions to ISO
10303-41 edition 2 are shown in pink and with a heavy outline.
The use of the entity general_property described in
3.2 Property space and
maths space.
There are many possible meanings for a relationship between a
property_value and a product_definition. For example, the
relationship can record that 99.9% of widgets of type XYZ have a mass between
9.99 and 10.01 Kg; or that the average mass for each batch of 100 widgets of
type XYZ is between 9.99 and 10.01.
The different meanings are distinguished by different subtypes or attributes of
property_definition.
Properties of actions are handled in exactly the same way as properties of products.
Mathematics is concerned with abstract quantities, so it is natural to associate maths_value (a mathematical abstraction) with property_value (a physical abstraction) which is independent of any product_definition.
ASIDE - This is probably not the only way to use a maths_value, but it fits well with the approach to property distributions discussed in 4. A Property distribution.
The property_value that is the mass range 9.99 to 10.01 Kg is represented by the maths_value that is the real interval [9.99, 10.01], as shown in Figure 2.
Figure 2: Identification of a property
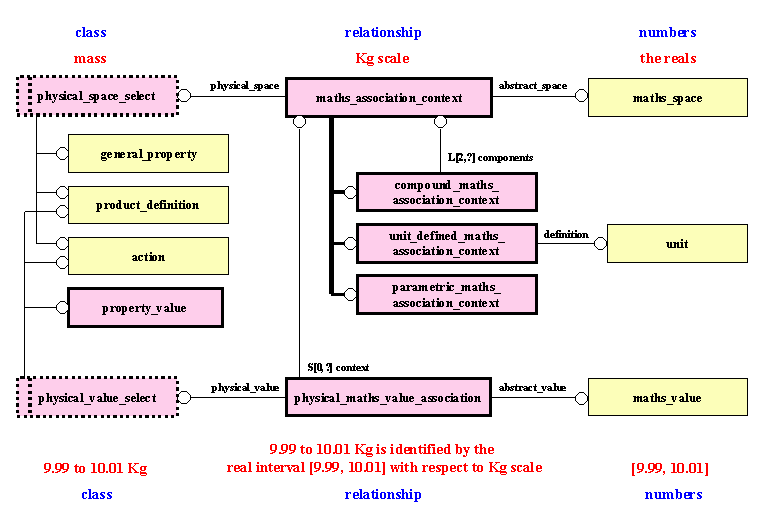
Notes:
The entity physical_maths_value_association has been added to specify the usage of a maths_value. The usage can be one of the following:
Some instances of property_value are represented by complicated instances of maths_value. For example a stress value is represented by a symmetric 3´3 matrix.
The entity maths_association_context indicates the meaning of the physical_maths_value_association and a usage of the maths_space. The usage can be one of the following:
The entity maths_association_context is discussed in detail in 3.2 Property space and maths space and 3.3 Parameterisation.
The identification of a property_value by a maths_value has a 'context' or scale. A scale relates each property_value within a property_space to a maths_value within a maths_space.
EXAMPLE - The kilogramme scale relates each mass value (i.e. each property_value within the mass property_space) to a real value (i.e. a maths_value within the maths_space of reals).
EXAMPLE - The Celsius scale relates each temperature value (i.e. each property_value within the temperature property_space) to a real value greater than -273.15 (i.e. a maths_value within the maths_space containing all reals greater than -273.15).
EXAMPLE - The MVAR scale relates each power (in an electrical transmission line) value (i.e. each property_value within the active and reactive power property_space) to a complex value (i.e. a maths_value within the maths_space of complex numbers).
Using the entities in Figure 2, a instance of unit_defined_maths_association_context specifies that:
The part 41 edition 2 entity general_property is understood to have exactly the same meaning as the EACM ARM entity property_space.
Until part 41 edition 2, STEP indicated the nature of a property space (such as position, time, mass, temperature, stress or strain) by an enumerated type or a text string. The recording of a property space by an entity is important for engineering analysis for the following reasons:
The last reason is important because it allows a reference to external dictionaries of property spaces that are held according to standards such as ISO 13584 (P-LIB). This capability is used within AP 214.
If the topology of widget type XYZ is simple, then we can define a mapping such that each point within widget type XYZ is identified by a triple of real numbers within the unit cube. This is shown by the instances at the top of Figure 4. The mapping between the set of points within widget type XYZ and the unit cube is a parameterisation.
The existence of a parameterisation is recorded by the entity parametric_maths_association_context in Figure 2. There are many possible parameterisations for any product or action, so it is necessary to specify which parameterisation is being used in the identification of a distribution.
A common form of parameterisation in engineering analysis is a mesh. A mesh over the volume of widget type XYZ provides a mapping such that each point within the widget was identified by:
The entity parametric_maths_association_context records the existence of a parameterisation but does not record 'what it is'. An understanding of 'what a parameterisation is' is best provided by a position in space distribution with respect to the parameterisation.
Such a distribution assigns a position in space to each parametric position within the product. This is what is shown on the screen when a finite element mesh is plotted.
NOTE - In finite element analysis, the derivative of position in space with respect to parametric position is called the 'Jacobian'.
A variation of density from point to point within widget type XYZ is a property distribution. This is a distribution over the set (infinite and uncountable) of points within widget type XYZ, such that a density value is assigned to each point.
A property distribution need not be over a set of points. The variation of bending moment along a beam B_123 is a property distribution. This is a distribution over the set (also infinite and uncountable) of cross sections within beam B_123, such that a bending moment value is assigned to each cross section.
The use of ISO 10303-41 edition 2 to record a property distribution is shown in Figure 3.
Figure 3: A property distribution
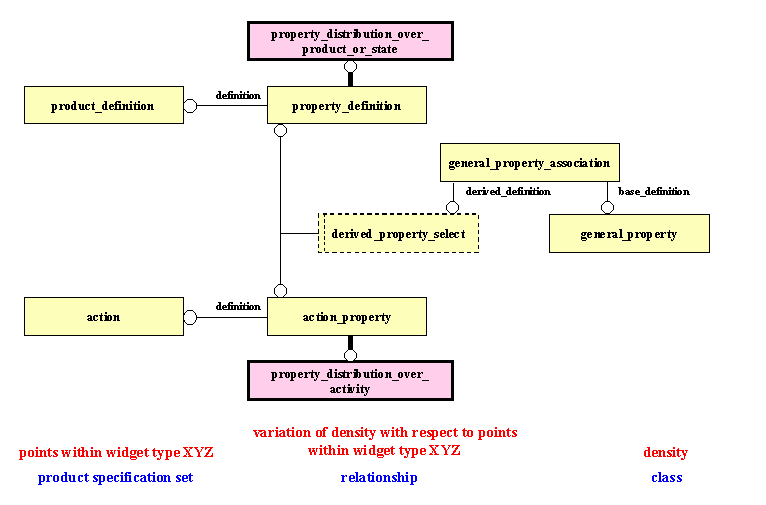
This approach to a property distribution is derived from the approach shown in Figure 1, by the following transformation:
The use of property_definition, as a property distribution, is indicated by the subtype property_distribution_over_product_or_state. (The 'or_state' is added to the entity name, because a product_definition can be for a product in a particular state, rather than for a product throughout its life.)
Subtypes of product_definition are also required, to indicate whether it is regarded as a whole, as a set of points (volume view), as a set of fibres (shell view) or as a set of cross-sections (beam view). These subtypes are not within the scope of this document.
NOTE - Only distributions with respect to position within a product are discussed here. The entity property_distribution_over_activity can be used in an analogous way to record distributions with respect to state within an activity.
Using mathematical terminology, a property distribution is a 'physical function' that has:
The physical function is represented by a maths_function that has:
The identification of a physical function by a maths_function is shown in Figure 4.
Figure 4: Identification of a property distribution
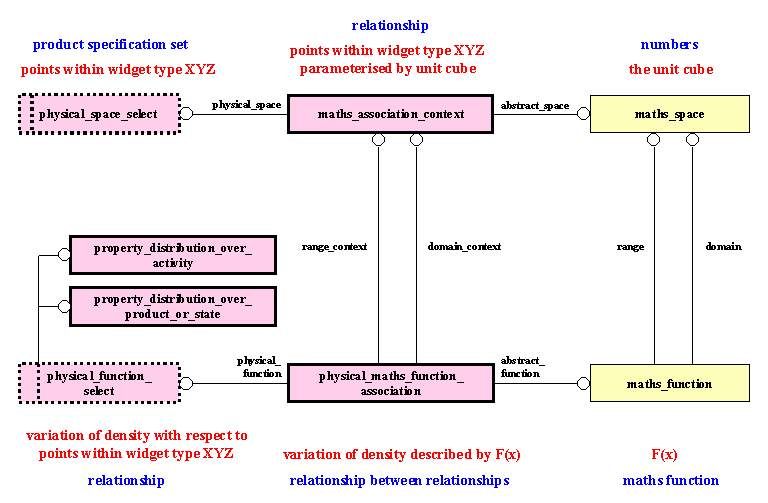
Notes:
The relationship between a property distribution and a maths_function is provided by the entity physical_maths_function_association.
A physical_maths_function_association requires two different 'contexts' - the scale which is described in 3.2 Property space and maths space and the parameterisation which is described in 3.3 Parameterisation.