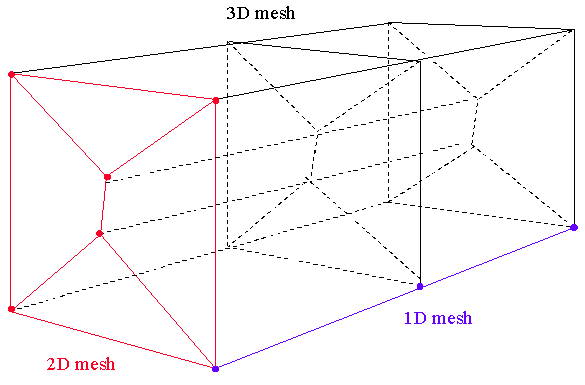
EXAMPLE - A product of a 2 dimensional mesh consisting of 4 cells and a 1 dimensional mesh consisting of 2 cells is shown in Figure 1.
Figure 1: A Product_of_mesh between a 2D mesh and a 1D
mesh
A Product_of_mesh is a relationship that is between:
and that indicates the n+1 dimensional Mesh is the Cartesian product of the operands.
The ordering of cells and vertices of the product Mesh is as follows:
EXAMPLE - A product of a 2 dimensional mesh consisting of 4 cells and a 1 dimensional mesh consisting of 2 cells is shown in Figure 1.
Figure 1: A Product_of_mesh between a 2D mesh and a 1D mesh

EXPRESS specification:
*)
ENTITY product_of_mesh;
operands : LIST[2,2] OF Mesh
product : Mesh;
WHERE
consistent_topological_dimension :
IF ('MESH_ARM.REGION' IN TYPEOF(operands[1])) AND
('MESH_ARM.REGION' IN TYPEOF(operands[2])) AND
('MESH_ARM.REGION' IN TYPEOF(product)) THEN
operands[1]\Region.topological_dimension +
operands[2]\Region.topological_dimension =
product\Region.topological_dimension;
ELSE
FALSE;
ENDIF;
single_dimensional_operand :
IF ('MESH_ARM.REGION' IN TYPEOF(operands[1])) AND
('MESH_ARM.REGION' IN TYPEOF(operands[2])) THEN
operands[1]\Region.topological_dimension = 1 OR
operands[2]\Region.topological_dimension = 1;
ELSE
FALSE;
ENDIF;
END_ENTITY;
(*
Attribute definitions:
operands: the instances of Mesh that define the product.
product: the Mesh that is the Cartesian product of the operands.
Formal propositions:
consistent_dimensions: the sum of the topological_dimension for each of the operands shall be equal to the topological_dimension of the product.
single_dimensional_operand: one of the operands shall have a topological_dimension equal to 1.